数据结构 图

定义-各种分类

图（Graph）：由顶点的非空有限集合 VV （由 n>0n>0 个顶点组成）与边的集合 EE（顶点之间的关系）构成的结构。其形式化定义为 G=(V,E)G=(V,E)。

  • 顶点（Vertex）：图中的数据元素通常称为顶点，在下面的示意图中我们使用圆圈来表示顶点。
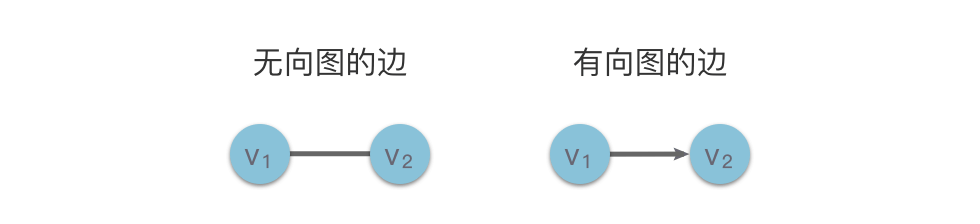
  • 边（Edge）：图中两个数据元素之间的关联关系通常称为边，在下面的示意图中我们使用连接两个顶点之间的线段来表示边。边的形式化定义为：e=⟨u,v⟩e=⟨u,v⟩，表示从 uu 到 vv 的一条边，其中 uu 称为起始点，vv 称为终止点。

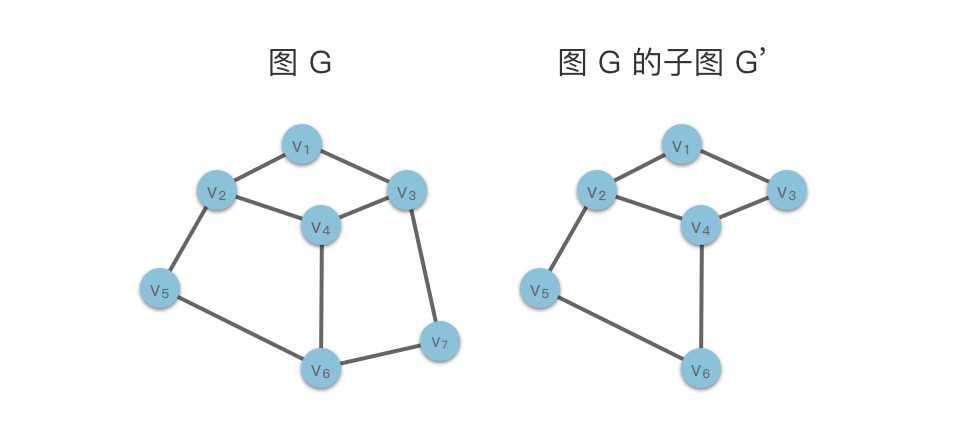
特别的，根据定义，GG 也是其自身的子图。

  • 无向图（Undirected Graph）：如果图中的每条边都没有指向性，则称为无向图。例如朋友关系图、路线图都是无向图。
  • 有向图（Directed Graph）：如果图中的每条边都具有指向性，则称为有向图。例如流程图是有向图。

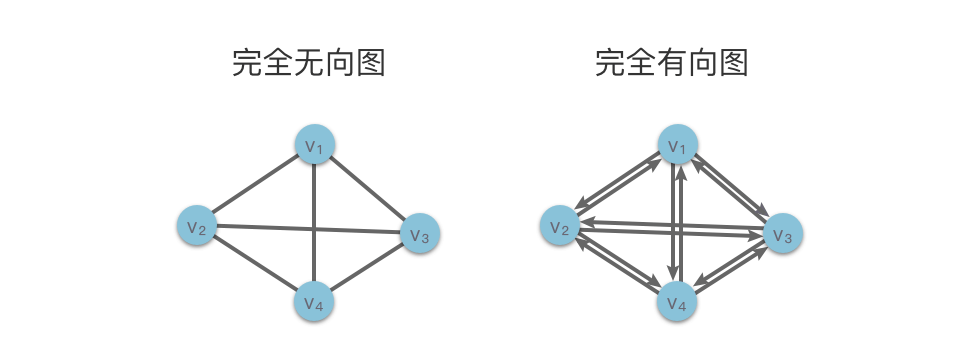
如果无向图中有 nn 个顶点，则无向图中最多有 n×(n−1)/2n×(n−1)/2 条边。而具有 n×(n−1)/2n×(n−1)/2 条边的无向图称为 「完全无向图（Completed Undirected Graph）」。

如果有向图中有 nn 个顶点，则有向图中最多有 n×(n−1)n×(n−1) 条弧。而具有 n×(n−1)n×(n−1) 条弧的有向图称为 「完全有向图（Completed Directed Graph）」。

说白了就是全都连起来了

  • 顶点的度：与该顶点 viv**i 相关联的边的条数，记为 TD(vi)T**D(v**i)。

例如上图左侧的完全无向图中，顶点 v3的度为 3。

而对于有向图，我们可以将顶点的度分为 「顶点的出度」 和 「顶点的入度」。

  • 顶点的出度：以该顶点 viv**i 为出发点的边的条数，记为 OD(vi)O**D(v**i)。
  • 顶点的入度：以该顶点 viv**i 为终止点的边的条数，记为 ID(vi)I**D(v**i)。
  • 有向图中某顶点的度 = 该顶点的出度 + 该顶点的入度，即 TD(vi)=OD(vi)+ID(vi)T**D(v**i)=O**D(v**i)+I**D(v**i)。

例如顶点v3的度就是6，3+3=6

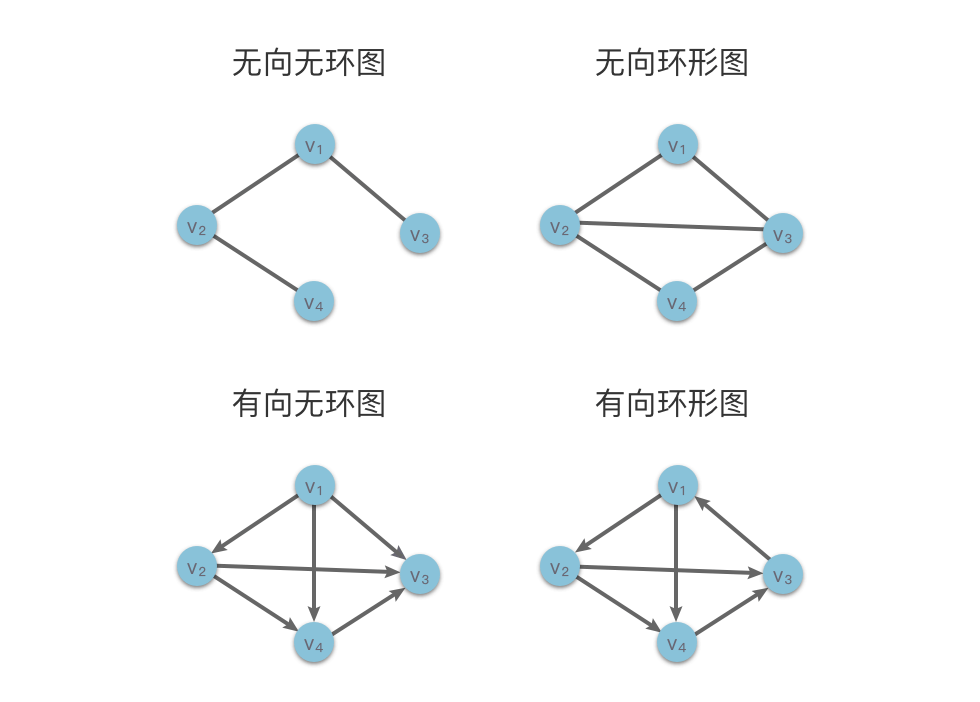
  • 环（Circle）：如果一条路径的起始点和终止点相同（即 vi0==vimv**i0==vim ），则称这条路径为「回路」或者「环」。

  • 简单路径：顶点序列中顶点不重复出现的路径称为「简单路径」。

而根据图中是否有环，我们可以将图分为「环形图」和「无环图」。

  • 环形图（Circular Graph）：如果图中存在至少一条环路，则该图称为「环形图」。
  • 无环图（Acyclic Graph）：如果图中不存在环路，则该图称为「无环图」。

在无向图中，如果从顶点 viv**i 到顶点 vjv**j 有路径，则称顶点 viv**i 和 vjv**j 是连通的。

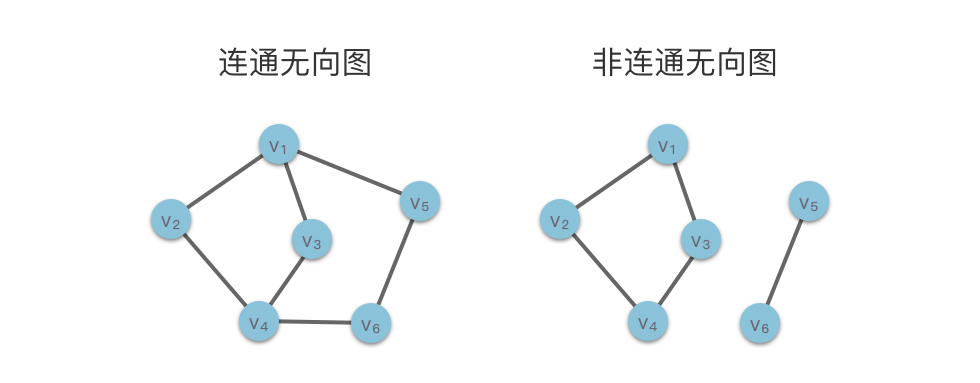
  • 连通无向图：在无向图中，如果图中任意两个顶点之间都是连通的，则称该图为连通无向图。
  • 非连通无向图：在无向图中，如果图中至少存在一对顶点之间不存在任何路径，则该图称为非连通无向图。

有些无向图可能不是连通无向图，但是其子图可能是连通的。这些子图称为原图的连通子图。而无向图的一个极大连通子图（不存在包含它的更大的连通子图）则称为该图的「连通分量」。

  • 连通子图：如果无向图的子图是连通无向图，则该子图称为原图的连通子图。

  • 连通分量：无向图中的一个极大连通子图（不存在包含它的更大的连通子图）称为该图的连通分量。

  • 极⼤连通⼦图：无向图中的一个连通子图，并且不存在包含它的更大的连通子图。

  • 强连通有向图：如果图中任意两个顶点 viv**i 和 vjv**j，从 viv**i 到 vjv**j 和从 vjv**j 到 viv**i 都有路径，则称该图为强连通有向图。

  • 非强连通有向图：如果图中至少存在一对顶点之间不存在任何路径，则该图称为非强连通有向图。

与无向图类似，有向图的一个极大强连通子图称为该图的 强连通分量。

  • 强连通子图：如果有向图的子图是连通有向图，则该子图称为原图的强连通子图。
  • 强连通分量：有向图中的一个极⼤强连通⼦图，称为该图的强连通分量。
  • 极⼤强连通⼦图：有向图中的一个强连通子图，并且不存在包含它的更大的强连通子图。

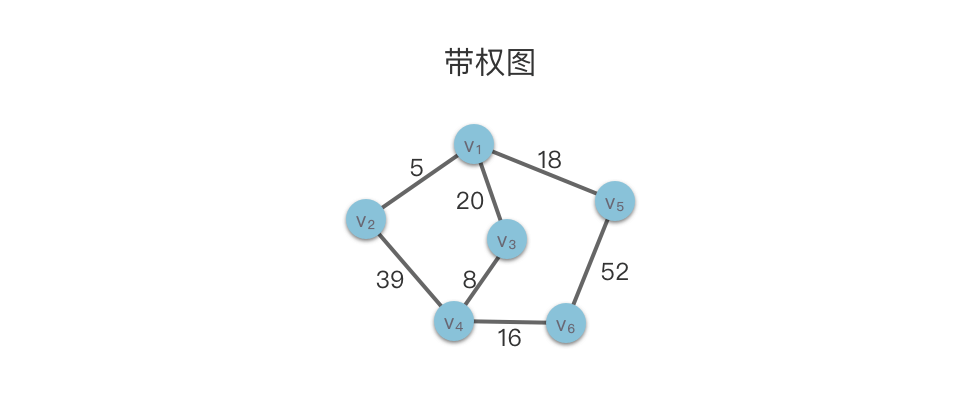
有时，图不仅需要表示顶点之间是否存在某种关系，还需要表示这一关系的具体细节。这时候我们需要在边上带一些数据信息，这些数据信息被称为 权。在具体应用中，权值可以具有某种具体意义，比如权值可以代表距离、时间以及价格等不同属性。

  • 带权图：如果图的每条边都被赋以⼀个权值，这种图称为带权图。
  • 网络：带权的连通⽆向图称为⽹络。

根据图中边的稀疏程度，我们可以将图分为「稠密图」和「稀疏图」。这是一个模糊的概念，目前为止还没有给出一个量化的定义。

  • 稠密图（Dense Graph）：有很多条边或弧（边的条数 ee 接近于完全图的边数）的图称为稠密图。
  • 稀疏图（Sparse Graph）：有很少条边或弧（边的条数 ee 远小于完全图的边数，如 e<n×log⁡2ne<n×log2n）的图称为稀疏图。

存储结构

我们在实现图的存储时，重点需要关注边与顶点之间的关联关系，这是图的存储的关键。

图的存储可以通过「顺序存储结构」和「链式存储结构」来实现。其中顺序存储结构包括邻接矩阵和边集数组。链式存储结构包括邻接表、链式前向星、十字链表和邻接多重表。

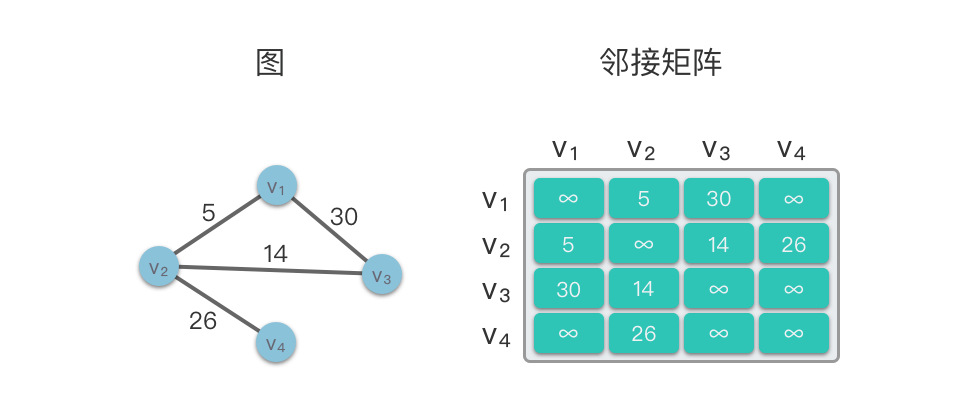
邻接矩阵

邻接矩阵（Adjacency Matrix）：使用一个二维数组 adj‾matrixadjmatri**x 来存储顶点之间的邻接关系。

  • 对于无权图来说，如果 adj‾matrix[i][j]adjmatri**x[i][j] 为 11，则说明顶点 viv**i 到 vjv**j 存在边，如果 adj‾matrix[i][j]adjmatri**x[i][j] 为 00，则说明顶点 viv**i 到 vjv**j 不存在边。
  • 对于带权图来说，如果 adj‾matrix[i][j]adjmatri**x[i][j] 为 ww，并且 w≠∞w\=∞（即 w != float('inf')），则说明顶点 viv**i 到 vjv**j 的权值为 ww。如果 adj‾matrix[i][j]adjmatri**x[i][j] 为 ∞∞（即 float('inf')），则说明顶点 viv**i 到 vjv**j 不存在边。

邻接矩阵的特点：

  • 优点：实现简单，并且可以直接查询顶点 viv**i 与 vjv**j 之间是否有边存在，还可以直接查询边的权值。

  • 缺点：初始化效率和遍历效率较低，空间开销大，空间利用率低，并且不能存储重复边，也不便于增删节点。如果当顶点数目过大（比如当 n>105n>105）时，使用邻接矩阵建立一个 n×nn×n 的二维数组不太现实。

  • 时间复杂度：

    • 初始化操作：O(n2)O(n2)。
    • 查询、添加或删除边操作：O(1)O(1)。
    • 获取某个点的所有边操作：O(n)O(n)。
    • 图的遍历操作 ：O(n2)O(n2)。

  • 空间复杂度：O(n2)O(n2)。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import java.util.Arrays;

public class Graph {
    private int verCount;
    private Integer[][] adjMatrix;
    public Graph(int verCount){
        this.verCount = verCount;
        adjMatrix = new Integer[verCount][verCount];
        for (Integer[] row:adjMatrix){
            Arrays.fill(row,null);
        }
    }
    private boolean isValid(int v) {
        return 0 <= v && v < verCount; 
    }

    public void createGraph(int[][] edges){
        for (int[] edge:edges){
            addEdge(edge[0],edge[1],edge[2]);
        }
    }
    public void addEdge(int vi,int vj,int val){
        if (!isValid(vi) || !isValid(vj)){
            throw new IllegalArgumentException(vi+"or"+vj+"is not");
        }
        adjMatrix[vi][vj] = val;
    }
    public Integer getEdge(int vi,int vj){
        if (!isValid(vi) || !isValid(vj)){
            throw new IllegalArgumentException(vi+"or"+vj+"is not");
        }
        return adjMatrix[vi][vj];
    }
    public void printGraph(){
        for (int vi=0;vi<verCount;vi++){
            for (int vj=0;vj<verCount;vj++){
                Integer val = getEdge(vi,vj);
                if (val!=null){
                    System.out.println(vi + "-" + vj + "-" + val);
                }
            }
        }
    }

    public static void main(String[] args) {
        Graph graph = new Graph(5);
        int[][] edges = {
                {1, 2, 5},
                {2, 1, 5},
                {1, 3, 30},
                {3, 1, 30},
                {2, 3, 14},
                {3, 2, 14},
                {2, 4, 26},
                {4, 2, 26}
        };
        graph.createGraph(edges);
        graph.getEdge(3,4);
        graph.printGraph();
    }

}

我在写代码的时候，出现了一些小小的问题

主要是异常处理没完成的问题

1
if (!isValid(vi) || !isValid(vj))

应该是这个逻辑，我写错了，大家注意

return

1
2
3
4
5
6
7
8
9
null
1-2-5
1-3-30
2-1-5
2-3-14
2-4-26
3-1-30
3-2-14
4-2-26

稍微修改了下，把检测权给输出出来了

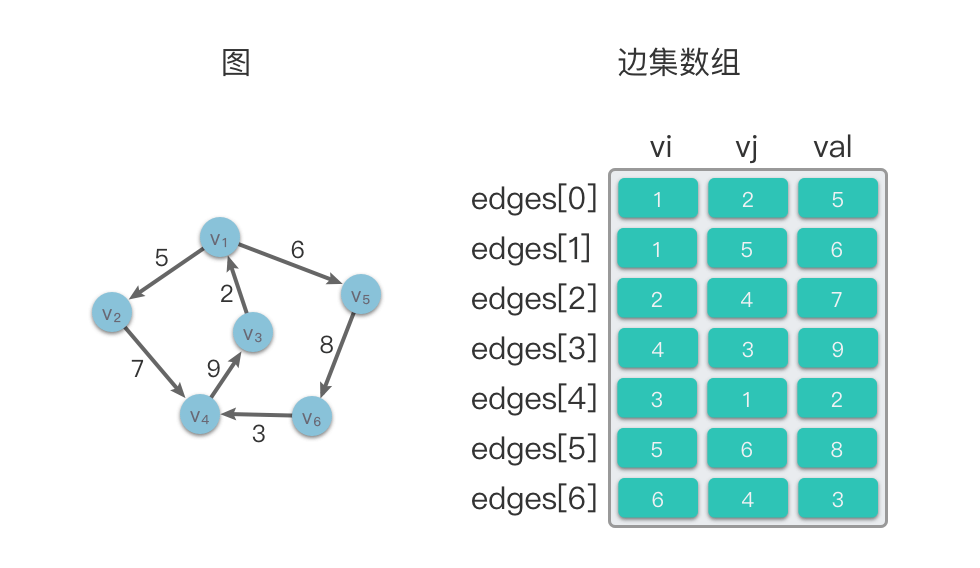
边集数组

边集数组（Edgeset Array）：使用一个数组来存储存储顶点之间的邻接关系。数组中每个元素都包含一条边的起点 viv**i、终点 vjv**j 和边的权值 valval（如果是带权图）。

边集数组的时间复杂度：

  • 图的初始化和创建操作：O(m)O(m)。
  • 查询是否存在某条边：O(m)O(m)。
  • 遍历某个点的所有边：O(m)O(m)。
  • 遍历整张图：O(nm)O(nm)。

边集数组的空间复杂度：

  • 空间复杂度：O(m)O(m)。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import java.util.ArrayList;
import java.util.List;

class EdgeNode{
    int vi;
    int vj;
    int val;

    public EdgeNode(int vi, int vj, int val) {
        this.vi = vi;
        this.vj = vj;
        this.val = val;
    }
}
public class EdgeListGraph {
    private List<EdgeNode> edges;
    public EdgeListGraph(){
        edges = new ArrayList<>();
    }
    public void  createGraph(int[][] edgesArray){
        for (int[] edge:edgesArray){
            addEdge(edge[0],edge[1],edge[2]);
        }
    }
    public void addEdge(int vi,int vj,int val){
        EdgeNode edge = new EdgeNode(vi,vj,val);
        edges.add(edge);
    }
    public Integer getEdge(int vi,int vj){
        for (EdgeNode edge:edges){
            if (vi==edge.vi&&vj==edge.vj){
                return edge.val;
            }
        }
        return null;
    }
    public void printGraph(){
        for (EdgeNode edge:edges){
            System.out.println(edge.vi + "-" + edge.vj + "-" + edge.val);
        }
    }

    public static void main(String[] args) {
        EdgeListGraph graph = new EdgeListGraph();
        int[][] edgesArray = {
                {1, 2, 5},
                {1, 5, 6},
                {2, 4, 7},
                {4, 3, 9},
                {3, 1, 2},
                {5, 6, 8},
                {6, 4, 3}
        };
        graph.createGraph(edgesArray);
        System.out.println(graph.getEdge(3, 4));
        graph.printGraph();
    }
}

return

1
2
3
4
5
6
7
8
null
1-2-5
1-5-6
2-4-7
4-3-9
3-1-2
5-6-8
6-4-3

一般来说，边集数组适合那些对边依次进行处理的运算，不适合对顶点的运算和对任何一条边的运算。

图的遍历

深度优先搜索

深度优先搜索算法（Depth First Search）：英文缩写为 DFS，是一种用于搜索树或图结构的算法。深度优先搜索算法采用了回溯思想，从起始节点开始，沿着一条路径尽可能深入地访问节点，直到无法继续前进时为止，然后回溯到上一个未访问的节点，继续深入搜索，直到完成整个搜索过程。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void depthFirstSearch(int start){
        boolean[] visited = new boolean[verCount];
        System.out.println("Dfs" + start + ":");
        dfsHelper(start,visited);
        System.out.println();
    }
    private void  dfsHelper(int vertex,boolean[] visited){
        visited[vertex] = true;
        System.out.println(vertex + " ");
        for (int vj=0;vj<verCount;vj++){
            if (adjMatrix[vertex][vj]!=null&&!visited[vj]){
                dfsHelper(vj,visited);
            }
        }
    }
1
2
3
4
5
Dfs4:
4 
2 
1 
3

但是一般使用递归的时候会出现不可控的错误

所以我们使用另一种方法

采用栈堆实现

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void DfsStack(int start){
        boolean[] visited = new boolean[verCount];
        Stack<Integer> stack = new Stack<>();
        stack.push(start);
        System.out.println("DFS is " + start + ":");
        while (!stack.isEmpty()){
            int vertex = stack.pop();
            if (!visited[vertex]){
                visited[vertex] = true;
                System.out.println(vertex + " ");
                for (int vj=0;vj<verCount;vj++){
                    if (adjMatrix[vertex][vj]!=null&&!visited[vj]){
                        stack.push(vj);
                    }
                }
            }
        }
    }

广度优先搜索

广度优先搜索算法（Breadth First Search）：英文缩写为 BFS，又译作宽度优先搜索 / 横向优先搜索，是一种用于搜索树或图结构的算法。广度优先搜索算法从起始节点开始，逐层扩展，先访问离起始节点最近的节点，后访问离起始节点稍远的节点。以此类推，直到完成整个搜索过程。

就是一层一层的访问呗

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void bfs(int start){
        boolean[] visited = new boolean[verCount];
        Queue<Integer> queue = new LinkedList<>();
        queue.add(start);
        visited[start] = true;
        System.out.println("Bfs" + start + " :");
        while (!queue.isEmpty()){
            int vertex = queue.poll();
            System.out.println(vertex + " ");
            for (int vj=0;vj<verCount;vj++){
                if (adjMatrix[vertex][vj]!=null&&!visited[vj]){
                    visited[vj] = true;
                    queue.add(vj);
                }
            }
        }
        System.out.println();
    }

可以借助队列来实现