数据结构 树篇

树的概念

树是一个有限的集合

我们的linux文件目录就是树状的

「树」具有以下的特点：

  • 有且仅有一个节点没有前驱节点，该节点被称为树的 「根节点（Root）」 。

  • 除了根节点以之，每个节点有且仅有一个直接前驱节点。

  • 包括根节点在内，每个节点可以有多个后继节点。

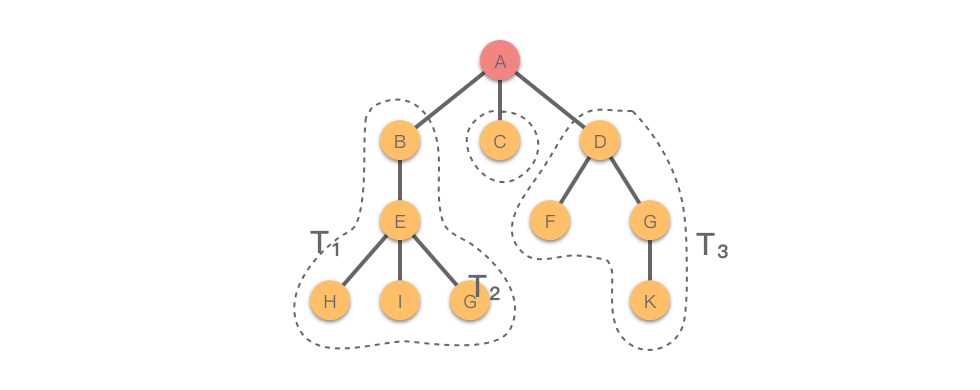
  • 当 n>1n>1 时，除了根节点之外的其他节点，可分为 m(m>0)m(m>0) 个互不相交的有限集合 T1,T2,…,TmT1,T2,…,T**m，其中每一个集合本身又是一棵树，并且被称为根的 「子树（SubTree）」。

    a

节点所含有的子树的个数就是节点的度

度为0的叫做叶子节点

度不为0的叫做分支节点

树中各节点的最大度数称为 「树的度」。

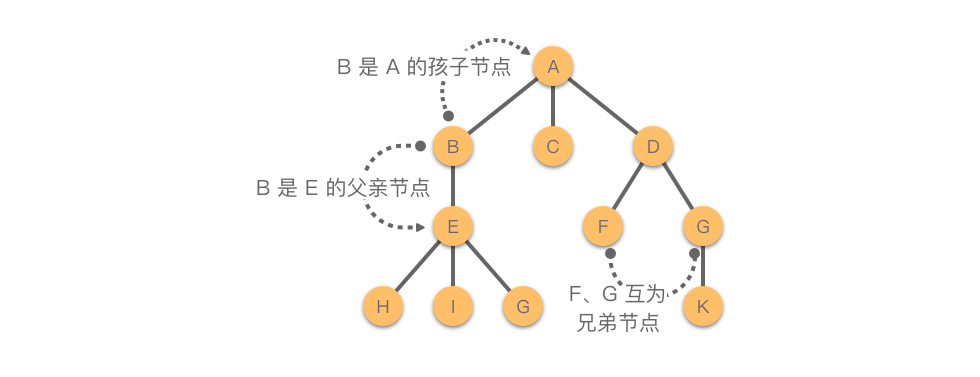
节点之间的关系

兄弟节点，孩子节点，父子节点…

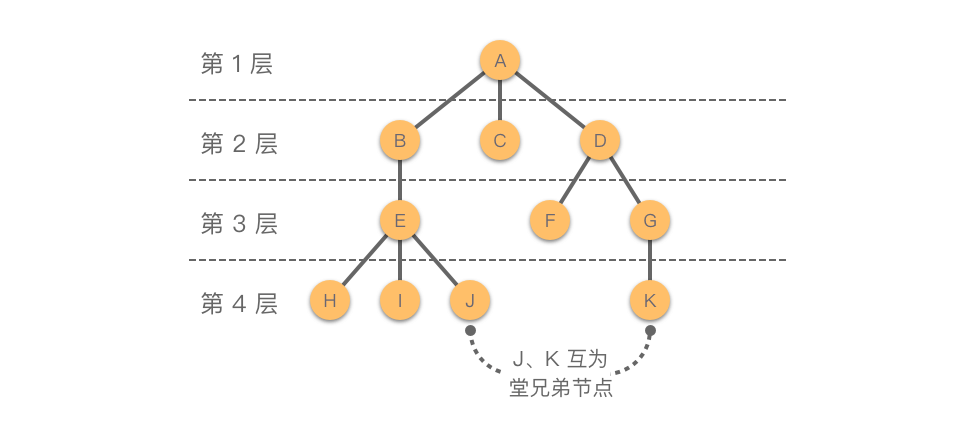
  • 节点的层次：从根节点开始定义，根为第 11 层，根的子节点为第 22 层，以此类推。
  • 树的深度（高度）：所有节点中最大的层数。例如图中树的深度为 44。
  • 堂兄弟节点：父节点在同一层的节点互为堂兄弟。例如图中 JJ、KK 互为堂兄弟节点。
  • 路径：树中两个节点之间所经过的节点序列。例如图中 EE 到 GG 的路径为 E−B−A−D−GE−B−A−D−G。
  • 路径长度：两个节点之间路径上经过的边数。例如图中 EE 到 GG 的路径长度为 44。
  • 节点的祖先：从该节点到根节点所经过的所有节点，被称为该节点的祖先。例如图中 HH 的祖先为 EE、BB、AA。
  • 节点的子孙：节点的子树中所有节点被称为该节点的子孙。例如图中 DD 的子孙为 FF、GG、KK。

树的分类

  • 有序树：节点的各个⼦树从左⾄右有序， 不能互换位置。
  • 无序树：节点的各个⼦树可互换位置。

二叉树

二叉树的简单实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}
class BinaryTree{
    TreeNode root;
    public BinaryTree(){
        root = null;
    }
    public  void insert(int val){
        root = insertRec(root,val);
    }
    private TreeNode insertRec(TreeNode root,int val){
        if (root==null){
            root = new TreeNode(val);
            return root;
        }
        if (val<root.val){
            root.left = insertRec(root.left,val);
        } else if (val>root.val){
            root.right = insertRec(root.right,val);
        }
        return root;
    }
    public void preOrder(){
        preOrderRec(root);
    }
    private void preOrderRec(TreeNode root){
        if (root!=null){
            System.out.println(root.val + " ");
            preOrderRec(root.left);
            preOrderRec(root.right);
        }
    }
    public void inOrder(){
        inOrderRec(root);
    }
    private void inOrderRec(TreeNode root){
        if (root != null){
            inOrderRec(root.left);
            System.out.println(root.val);
            inOrderRec(root.right);
        }
    }
    public void postOrder(){
        postOrderRec(root);
    }
    private void postOrderRec(TreeNode root){
        if (root!=null){
            postOrderRec(root.left);
            postOrderRec(root.right);
            System.out.println(root.val);
        }
    }
    public boolean search(int val){
        return search(root.val);
    }
    private boolean searchRec(TreeNode root,int val){
        if (root==null){
            return false;
        }
        if (root.val ==val){
            return true;
        }
        return val<root.val ? searchRec(root.left,val) : searchRec(root.right,val);
    }

}

public class tree_1 {
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.insert(50);
        tree.insert(30);
        tree.insert(20);
        tree.insert(40);
        tree.insert(70);
        tree.insert(60);
        tree.insert(80);
        tree.postOrder();
    }
}

后遍历输出结果：

1
20 40 30 60 80 70 50

当然这个是print的结果，我懒得改了宝贝们

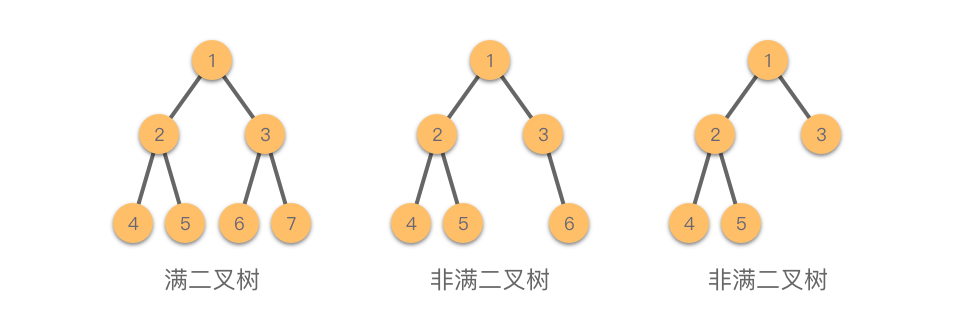
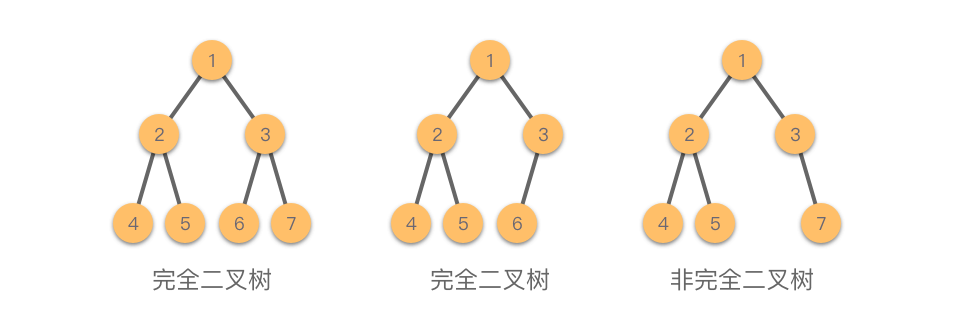
二叉树还有许许多多的分类。完全满不满的很多种

二叉树的遍历

二叉树的遍历：指的是从根节点出发，按照某种次序依次访问二叉树中所有节点，使得每个节点被访问一次且仅被访问一次。

一共有三种遍历方式

「二叉树的前序遍历」、「二叉树的中序遍历」 和 「二叉树的后续遍历」

前序遍历规则

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 访问根节点。
    2. 以前序遍历的方式遍历根节点的左子树。
    3. 以前序遍历的方式遍历根节点的右子树。
1
2
3
4
5
6
7
8
9
10
public void preOrder(){
        preOrderRec(root);
    }
    private void preOrderRec(TreeNode root){
        if (root!=null){
            System.out.println(root.val + " ");
            preOrderRec(root.left);
            preOrderRec(root.right);
        }
    }

代码实现

中序遍历规则

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 以中序遍历的方式遍历根节点的左子树。
    2. 访问根节点。
    3. 以中序遍历的方式遍历根节点的右子树。

代码实现

1
2
3
4
5
6
7
8
9
10
public void inOrder(){
        inOrderRec(root);
    }
    private void inOrderRec(TreeNode root){
        if (root != null){
            inOrderRec(root.left);
            System.out.println(root.val);
            inOrderRec(root.right);
        }
    }

后序遍历实现

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 以后序遍历的方式遍历根节点的左子树。
    2. 以后序遍历的方式遍历根节点的右子树。
    3. 访问根节点。

代码实现

1
2
3
4
5
6
7
8
9
10
public void postOrder(){
        postOrderRec(root);
    }
    private void postOrderRec(TreeNode root){
        if (root!=null){
            postOrderRec(root.left);
            postOrderRec(root.right);
            System.out.println(root.val);
        }
    }

层序遍历的实现

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 先依次访问二叉树第 11 层的节点。
    2. 然后依次访问二叉树第 22 层的节点。
    3. ……
    4. 依次下去，最后依次访问二叉树最下面一层的节点。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void levelOrder(){
        if (root ==null) return;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            System.out.println(node.val);
            if (node.left!=null){
                queue.add((node.left));
            }
            if (node.right!=null){
                queue.add(node.right);
            }
        }
    }

二叉树的还原

二叉树的还原：指的是通过二叉树的遍历序列，还原出对应的二叉树。

还原唯一性的确定：

如果已知一棵二叉树的前序序列和中序序列，可以唯一地确定这棵二叉树。

如果已知一棵二叉树的中序序列和后序序列，也可以唯一地确定这棵二叉树

已知二叉树的「中序遍历序列」和「层序遍历序列」，也可以唯一地确定一棵二叉树。

注意：

!!!

如果已知二叉树的「前序遍历序列」和「后序遍历序列」，是不能唯一地确定一棵二叉树的。 这是因为没有中序遍历序列无法确定左右部分，也就无法进行子序列的分割。

二叉搜索树

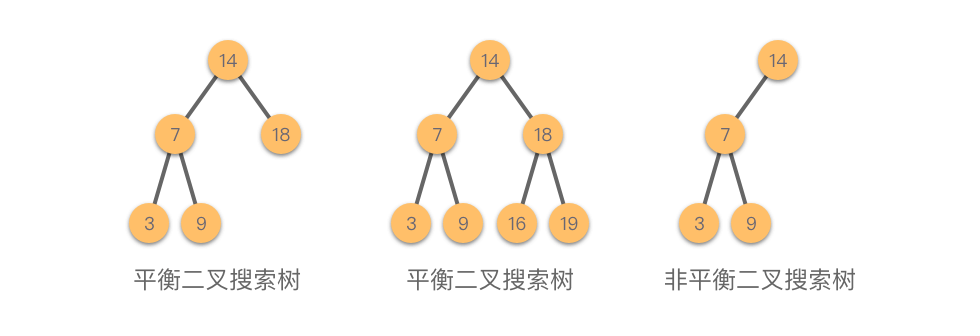
二叉搜索树（Binary Search Tree）：也叫做二叉查找树、有序二叉树或者排序二叉树。是指一棵空树或者具有下列性质的二叉树：

  • 如果任意节点的左子树不为空，则左子树上所有节点的值均小于等于它的根节点的值。
  • 如果任意节点的右子树不为空，则右子树上所有节点的值均大于等于它的根节点的值。
  • 任意节点的左子树、右子树均为二叉搜索树。

注意：

一般来说二叉搜索树中没有值相等的点，为了增加相等的点

可以加上等于的条件

查找算法的分析：

最好：O(log2n)

最坏：O(n)

平均：

在平均情况下，二叉搜索树的平均查找长度为 ASL=[(n+1)/n]∗/log2(n+1)−1ASL=[(n+1)/n]∗/log2(n+1)−1。所以二分搜索树的查找平均时间复杂度为 O(log2n)O(log2n)。

二叉搜索树的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
import java.util.LinkedList;
import java.util.Queue;

class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}
class BinaryTree {
    TreeNode root;

    public BinaryTree() {
        root = null;
    }

    public void insert(int val) {
        root = insertRec(root, val);
    }

    private TreeNode insertRec(TreeNode root, int val) {
        if (root == null) {
            root = new TreeNode(val);
            return root;
        }
        if (val < root.val) {
            root.left = insertRec(root.left, val);
        } else if (val > root.val) {
            root.right = insertRec(root.right, val);
        }
        return root;
    }

    public void preOrder() {
        preOrderRec(root);
    }

    private void preOrderRec(TreeNode root) {
        if (root != null) {
            System.out.println(root.val + " ");
            preOrderRec(root.left);
            preOrderRec(root.right);
        }
    }

    public void inOrder() {
        inOrderRec(root);
    }

    private void inOrderRec(TreeNode root) {
        if (root != null) {
            inOrderRec(root.left);
            System.out.println(root.val);
            inOrderRec(root.right);
        }
    }

    public void postOrder() {
        postOrderRec(root);
    }

    private void postOrderRec(TreeNode root) {
        if (root != null) {
            postOrderRec(root.left);
            postOrderRec(root.right);
            System.out.println(root.val);
        }
    }

    public void levelOrder() {
        if (root == null) return;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.println(node.val);
            if (node.left != null) {
                queue.add((node.left));
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }

    public boolean search(int val) {
        return search(root.val);
    }

    private boolean searchRec(TreeNode root, int val) {
        if (root == null) {
            return false;
        }
        if (root.val == val) {
            return true;
        }
        return val < root.val ? searchRec(root.left, val) : searchRec(root.right, val);
    }

    private int findMin(TreeNode root) {
        int min = root.val;
        while (root.left != null) {
            root = root.left;
            min = root.val;
        }
        return min;
    }

    public void delete(int val) {
        root = deleteRec(root, val);
    }

    private TreeNode deleteRec(TreeNode root, int val) {
        if (root == null) return null;
        if (val < root.val) {
            root.left = deleteRec(root.left, val);
        } else if (val > root.val) {
            root.right = deleteRec(root.right, val);
        } else {
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            root.val = findMin(root.right);
            root.right = deleteRec(root.right, root.val);
        }
        return root;
    }

    public class tree_1 {
        public static void main(String[] args) {
            BinaryTree tree = new BinaryTree();
            tree.insert(50);
            tree.insert(30);
            tree.insert(20);
            tree.insert(40);
            tree.insert(70);
            tree.insert(60);
            tree.insert(80);
            tree.postOrder();
        }
    }
}

完整的代码实现

线段树

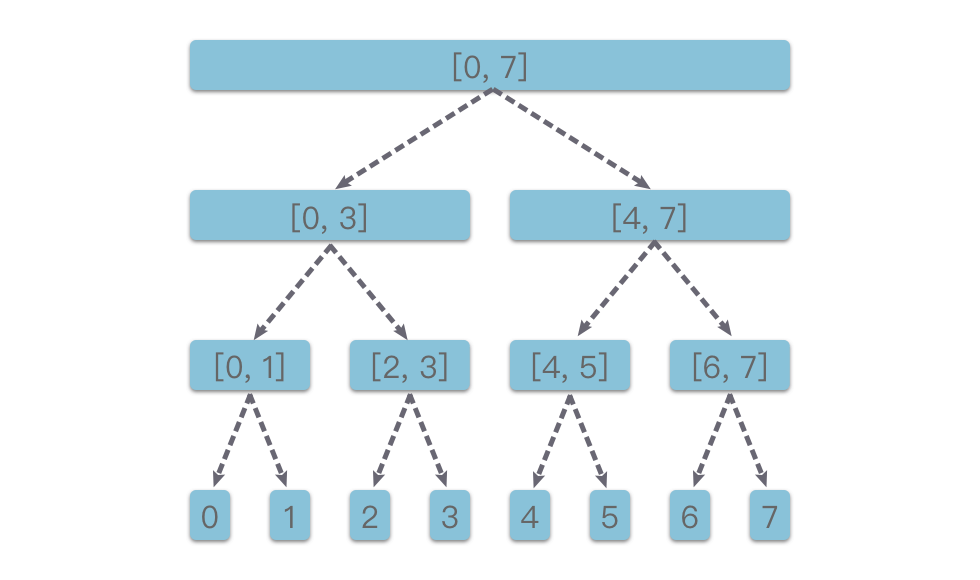
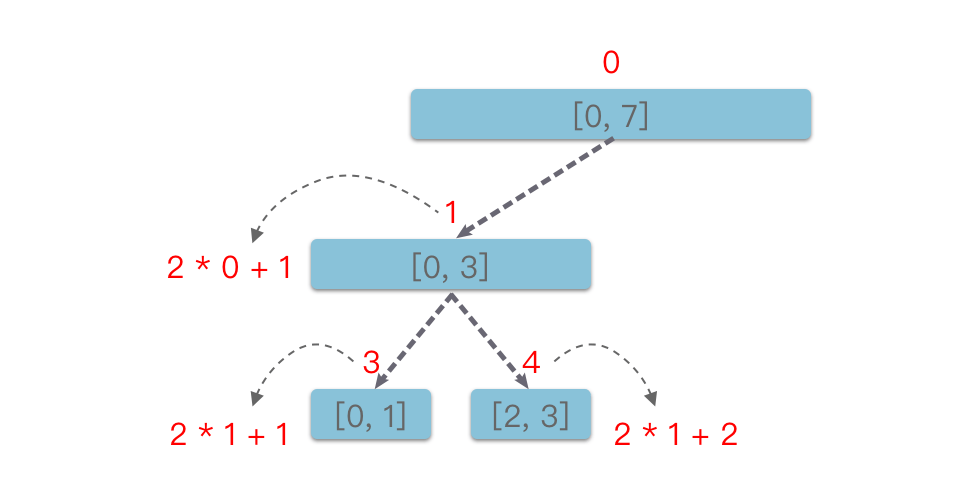
一种基于分治思想的二叉树，用于在区间上进行信息统计。它的每一个节点都对应一个区间 [left,right][lef**t,right] ，leftlef**t、rightright 通常是整数。每一个叶子节点表示了一个单位区间（长度为 11），叶子节点对应区间上 left==rightlef**t==right。每一个非叶子节点 [left,right][lef**t,right] 的左子节点表示的区间都为 [left,(left+right)/2][lef**t,(lef**t+right)/2]，右子节点表示的的区间都为 [(left+right)/2+1,right][(lef**t+right)/2+1,right]。

例如：

线段树的特点

  1. 线段树的每个节点都代表一个区间。
  2. 线段树具有唯一的根节点，代表的区间是整个统计范围，比如 [1,n][1,n]。
  3. 线段树的每个叶子节点都代表一个长度为 11 的单位区间 [x,x][x,x]。
  4. 对于每个内部节点 [left,right][lef**t,right]，它的左子节点是 [left,mid][lef**t,mi**d]，右子节点是 [mid+1,right][mi**d+1,right]。其中 mid=(left+right)/2mi**d=(lef**t+right)/2（向下取整）。

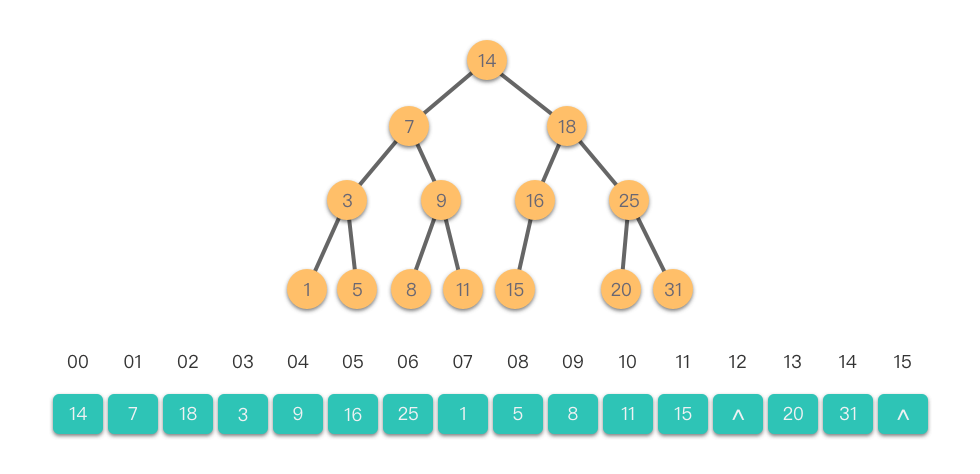
由于线段树近乎是完全二叉树，所以很适合用「顺序存储结构」来实现。

比如

  1. 如果是叶子节点（left==rightlef**t==right），则节点的值就是对应位置的元素值。
  2. 如果是非叶子节点，则递归创建左子树和右子树。
  3. 节点的区间值（区间和、区间最大值、区间最小值）等于该节点左右子节点元素值的对应计算结果。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
public class SegmentTree {
    private int tree[];
    private int data[];

    public SegmentTree(int[] nums) {
        if (nums.length > 0) {
            int n = nums.length;
            data = nums;
            tree = new int[4 * n];
            buildTree(0, 0, n - 1);
        }
    }

    private void buildTree(int node, int start, int end) {
        if (start == end) {
            tree[node] = data[start];
        } else {
            int mid = (start + end) / 2;
            int leftChild = 2 * node + 1;
            int rightChild = 2 * node + 2;
            buildTree(leftChild, start, mid);
            buildTree(rightChild, mid + 1, end);
            tree[node] = tree[leftChild] + tree[rightChild];
        }
    }

    public int query(int L, int R) {
        return queryRec(0, 0, data.length - 1, L, R);
    }

    private int queryRec(int node, int start, int end, int L, int R) {
        if (R < start || L > end) {
            return 0;
        }
        if (L <= start && end <= R) {
            return tree[node];
        }
        int mid = (start + end) / 2;
        int leftChild = 2 * node + 1;
        int rightChild = 2 * node + 2;
        int leftSum = queryRec(leftChild, start, mid, L, R);
        int rightSum = queryRec(rightChild, mid + 1, end, L, R);
        return leftSum + rightSum;
    }
    public void update(int index,int val){
        updateRec(0,0,data.length-1,index,val);
    }
    private void updateRec(int node,int start,int end,int index,int val) {
        if (start == end) {
            data[index] = val;
            tree[node] = val;
        } else {
            int mid = (start + end) / 2;
            int leftChild = 2 * node + 1;
            int rightChild = 2 * node + 2;
            if (index <= mid) {
                // 更新左子树
                updateRec(leftChild, start, mid, index, val);
            } else {
                // 更新右子树
                updateRec(rightChild, mid + 1, end, index, val);
            }
            tree[node] = tree[leftChild] + tree[rightChild];
        }
    }
}

红黑树

红黑树（Red-Black Tree）是一种自平衡二叉搜索树，在插入和删除节点时通过一些规则保持树的平衡，避免树的高度过高，从而保证增删查的时间复杂度为 O(log n)。

红黑树的性质：

每个节点要么是红色的，要么是黑色的。

根节点必须是黑色的。

每个叶节点（NIL节点，虚拟节点）是黑色的。

如果一个节点是红色的，那么它的两个子节点必须是黑色的（不能有两个连续的红色节点）。

从任意一个节点到其每个叶节点的路径都包含相同数目的黑色节点（黑高，即从根到叶子所有路径上的黑色节点数量相同）。

其最坏时间复杂度就是O(log n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
 class RedBlackTree {
    private static final boolean RED = true;
    private static final boolean BLACK  = false;
    private class Node{
        int key;
        Node left,right,parent;
        boolean color;
        Node(int key){
            this.key = key;
            this.color = RED;
        }
    }
    private Node root;
    private void leftRotate(Node x){//左旋
        Node y =x.right;
        x.right =y.left;
        if (y.left!=null){
            y.left.parent=x;
        }
        y.parent = x.parent;
        if (x.parent==null){
            root=y;
        }else if (x==x.parent.left){
            x.parent.left = y;
        }else {
            x.parent.right = y;
        }
        y.left = x;
        x.parent = y;
    }

}

红黑树左旋代码实现（（（好难啊）））

并查集

一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。不交集指的是一系列没有重复元素的集合。

并查集主要支持两种操作：

  • 合并（Union）：将两个集合合并成一个集合。
  • 查找（Find）：确定某个元素属于哪个集合。通常是返回集合内的一个「代表元素」。

代码实现：

使用快速查询

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class UnionFind {
    private int[] parent;
    private int[] rank;

    public UnionFind(int size) {
        parent = new int[size];
        rank = new int[size];
        for (int i=0;i<size;i++){
            parent[i] = i;
            rank[i] =1;
        }
    }
    public int find(int p){
        if (parent[p]!=p){
            parent[p] = find(parent[p]);
        }
        return parent[p];
    }
    public void union(int p,int q){
        int rootP = find(p);
        int rootQ = find(q);
        if (rootQ!=rootP){
            if (rank[rootP]>rank[rootQ]){
                parent[rootQ] = rootP;
            }else if (rank[rootP]<rank[rootQ]){
                parent[rootP] = rootQ;
            }else {
                parent[rootQ] = rootP;
                rank[rootP]++;
            }
        }
    }
    public boolean connected(int p,int q){
        return find(p) ==find(q);
    }

    public static void main(String[] args) {
        UnionFind unionFind = new UnionFind(10);
        unionFind.union(1,2);
        unionFind.union(2,3);
        System.out.println(unionFind.connected(1, 3));
        System.out.println(unionFind.connected(1, 4));

    }
}

return

1
2
true
false

说明1.3和1,2有交集

而2,3和1,4没有交集

在find 方法里运用了路径压缩的知识

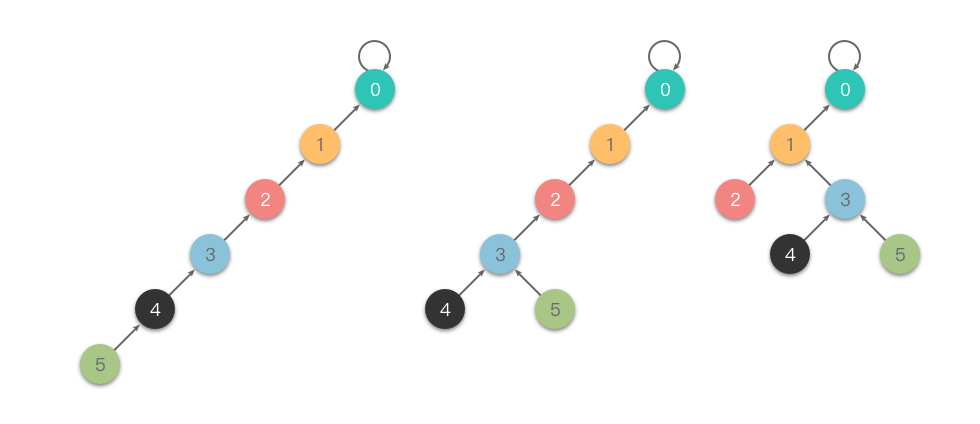
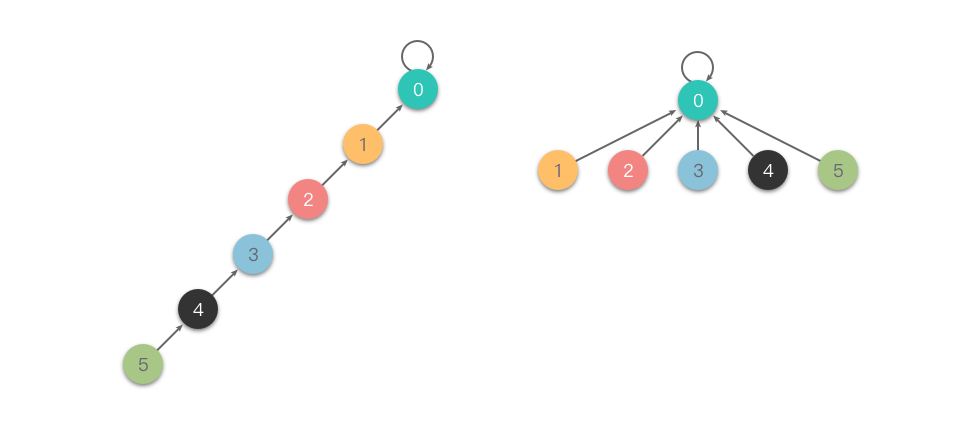
路径压缩: 在查找的过程中，使用递归方式将当前节点的父节点指向根节点，以降低树的深度，提高查找效率。这一步骤可以将树的高度压缩为接近常数，极大地优化查询操作的效率。

1
2
3
4
5
6
7
public int find(int p){
    if (parent[p]!=p){
        parent[p] = find(parent[p]); // 路径压缩
    }
    return parent[p];
}

union 方法用于将两个元素 p 和 q 所属的集合进行合并。

首先使用 find 方法找到两个元素的根节点 rootP 和 rootQ。

如果这两个元素的根节点不同，则说明它们属于不同的集合，需要将它们合并：

  • 根据两个根节点的 rank 来决定合并方向：将rank较小的树连接到rank较大的树上，从而保持树的扁平。
  • 如果两个集合的 rank 相等，则任选一个作为父节点，同时将它的 rank 值加一。

联通来比较他们的根节点是不是相同

最后来一个main的测试方法

来了两种路径压缩的方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public class UninFind {
    private int[] parent;
    private int[] rank;

    public UninFind(int size) {
        parent = new int[size];
        rank = new int[size];
        for (int i=0;i<size;i++){
            parent[i] = i;
            rank[i] =1;
        }
    }
    public int find1(int p){//完全压缩
        if (parent[p]!=p){
            parent[p] = find1(parent[p]);
        }
        return parent[p];
    }
    public int find2(int p){//隔代压缩
        if (parent[p]!=p){
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;
    }
    public void union(int p,int q){
        int rootP = find1(p);
        int rootQ = find1(q);
        if (rootQ!=rootP){
            if (rank[rootP]>rank[rootQ]){
                parent[rootQ] = rootP;
            }else if (rank[rootP]<rank[rootQ]){
                parent[rootP] = rootQ;
            }else {
                parent[rootQ] = rootP;
                rank[rootP]++;
            }
        }
    }
    public boolean connected(int p,int q){
        return find1(p) ==find1(q);
    }

    public static void main(String[] args) {
        UninFind unionFind = new UninFind(10);
        unionFind.union(1,2);
        unionFind.union(2,3);
        System.out.println(unionFind.connected(1, 3));
        System.out.println(unionFind.connected(1, 4));

    }
}

示意图如下

隔代压缩

完全压缩

按秩合并

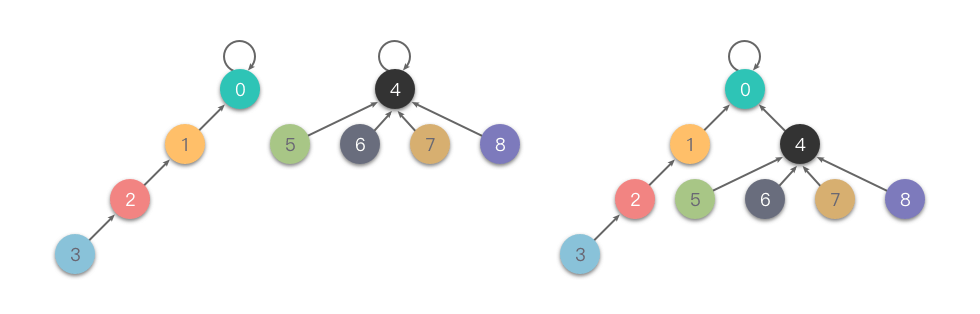
因为路径压缩只在查询时进行，并且只压缩一棵树上的路径，所以并查集最终的结构仍然可能是比较复杂的。为了避免这种情况，另一个优化方式是「按秩合并」

指的是在每次合并操作时，都把「秩」较小的树根节点指向「秩」较大的树根节点。

一种叫做「按深度合并」；另一种叫做「按大小合并」。

按秩合并的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
public class UninFind {
    private int[] parent;
    private int[] rank;
    private int[] size;

    public UninFind(int size) {
        parent = new int[size];
        rank = new int[size];
        this.size = new int[size];
        for (int i=0;i<size;i++){
            parent[i] = i;
            rank[i] =1;
            this.size[i] =1;
        }
    }
    public int find1(int p){//完全压缩
        if (parent[p]!=p){
            parent[p] = find1(parent[p]);
        }
        return parent[p];
    }
    public int find2(int p){//隔代压缩
        if (parent[p]!=p){
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;
    }
    public void unionBySize(int p,int q){//按大小合并
        int rootP = find1(p);
        int rootQ = find1(q);
        if (rootP!=rootP){
            if (size[rootP]>size[rootQ]){
                parent[rootQ] = rootP;
                size[rootP]+=size[rootQ];
            } else {
                parent[rootP] =rootQ;
                size[rootQ] +=size[rootP];
            }
        }
    }
    public void unionByRank(int p,int q){//按深度合并
        int rootP = find1(p);
        int rootQ = find1(q);
        if (rootQ!=rootP){
            if (rank[rootP]>rank[rootQ]){
                parent[rootQ] = rootP;
            }else if (rank[rootP]<rank[rootQ]){
                parent[rootP] = rootQ;
            }else {
                parent[rootQ] = rootP;
                rank[rootP]++;
            }
        }
    }
    public boolean connected(int p,int q){
        return find1(p) ==find1(q);
    }

    public static void main(String[] args) {
        UninFind unionFind = new UninFind(10);
        unionFind.unionByRank(1,2);
        unionFind.unionByRank(2,3);
        System.out.println(unionFind.connected(1, 3));
        System.out.println(unionFind.connected(1, 4));

    }
}

按深度合并

按深度合并

按大小合并

综上：

  • 并查集的空间复杂度：O(n)O(n)。
  • 并查集的时间复杂度：O(m×α(n))O(m×α(n))。

霍夫曼树

设二叉树具有 n 个带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度

设 w_i 为二叉树第 i 个叶结点的权值，l_i 为从根结点到第 i 个叶结点的路径长度，则 WPL 计算公式如下：

WPL=um_{i=1}^nw_il_i

img

如上图所示，其 WPL 计算过程与结果如下

1
2*2+3*2+4*2+7*2=32

对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中，WPL 最小的二叉树 称为 霍夫曼树（Huffman Tree）。

对于霍夫曼树来说，其叶结点权值越小，离根越远，叶结点权值越大，离根越近，此外其仅有叶结点的度为 0，其他结点度均为 2。

霍夫曼树可用于构造 最短的前缀编码，即 霍夫曼编码（Huffman Code），其构造步骤如下：

  1. 设需要编码的字符集为：d_1,d_2,ots,d_n，他们在字符串中出现的频率为：w_1,w_2,ots,w_n。
  2. 以 d_1,d_2,ots,d_n 作为叶结点，w_1,w_2,ots,w_n 作为叶结点的权值，构造一棵霍夫曼树。
  3. 规定哈夫曼编码树的左分支代表 0，右分支代表 1，则从根结点到每个叶结点所经过的路径组成的 0、1 序列即为该叶结点对应字符的编码。

霍夫曼树的构建：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import java.util.PriorityQueue;

class HuffmanNode implements Comparable<HuffmanNode> {
    char ch;
    int frequency;
    HuffmanNode left;
    HuffmanNode right;

    public HuffmanNode(char ch, int frequency) {
        this.ch = ch;
        this.frequency = frequency;
    }

    @Override
    public int compareTo(HuffmanNode node) {
        return this.frequency - node.frequency;
    }
}

public class HuffmanTree {

    public static HuffmanNode buildHuffmanTree(char[] chars, int[] frequencies) {
        PriorityQueue<HuffmanNode> priorityQueue = new PriorityQueue<>();

        // 构造初始节点并加入优先队列
        for (int i = 0; i < chars.length; i++) {
            priorityQueue.add(new HuffmanNode(chars[i], frequencies[i]));
        }

        // 构建霍夫曼树
        while (priorityQueue.size() > 1) {
            HuffmanNode left = priorityQueue.poll();
            HuffmanNode right = priorityQueue.poll();

            // 新节点频率为左右子节点之和，字符设为占位符（如'-'）
            HuffmanNode parent = new HuffmanNode('-', left.frequency + right.frequency);
            parent.left = left;
            parent.right = right;

            priorityQueue.add(parent);
        }

        return priorityQueue.poll();
    }

    public static void printHuffmanCodes(HuffmanNode root, String code) {
        if (root == null) { // 修正条件：若root为null，则直接返回
            return;
        }

        // 如果当前节点是叶子节点，打印编码
        if (root.left == null && root.right == null) {
            System.out.println(root.ch + ": " + code);
            return;
        }

        // 递归遍历左、右子树
        printHuffmanCodes(root.left, code + "0");
        printHuffmanCodes(root.right, code + "1");
    }

    public static void main(String[] args) {
        char[] chars = {'a', 'b', 'c', 'd', 'e', 'f'};
        int[] frequencies = {5, 9, 12, 13, 16, 45};

        // 构建霍夫曼树
        HuffmanNode root = buildHuffmanTree(chars, frequencies);

        System.out.println("霍夫曼编码：");
        printHuffmanCodes(root, "");
    }
}


return

1
2
3
4
5
6
7
8
9
霍夫曼编码：
f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111

进程已结束，退出代码为 0